Math Kit

Math Kit

数学を学ぶためのキットが揃っています。「途中式を飛ばさない」数学学習サイトとなっています。ぜひ、学習に役立たせてください。

2021-09-04

「私は嘘つきである」変なのわかる？パラドックス「モンティホール問題」

雑談

はじめに
- パラドックスとは
モンティ・ホール問題とは？
- どんなゲームだったのか？
- 天才現れる
解説
- 解説①　理論的に理解する
- 解説② 　ドアを100個に増やして感覚的に理解する
おわりに
Math Kit

はじめに

みなさんこんにちは！

パラドックス問題って聞いたことがありますか？

今回は、ある有名なパラドックス問題と一人の天才のお話になっています。

パラドックスとは

パラドックスとは、正しく見える前提や論理から、納得しがたい結論が導かれてしまう問題のことを言います。

一つ例を紹介しましょう。

「私は嘘つきである。」という言葉を考えていきましょう。

なんの変哲もない言葉に思えますし、何気ない友達との会話の中にも出てきそうな言葉ですね。

しかし、よくよく見てみるとおかしな言葉です。

①「私」が本当に嘘つきだとする

この言葉も嘘になるので、「私」は正直者である。

②「私」が本当は正直者だとする。

この言葉は本当になるので、「私」は嘘つきである。

それぞれの仮定と結論が矛盾します。

①

仮定：「私」が嘘つきだとする。

結論：「私」は正直者である。

②

仮定：「私」が正直者だとする。

結論：「私」は嘘つきである。

このように、ぱっと見は簡単そうなものも論理的に展開してみるとそうではないものをパラドックスと言われ、興味深い問題が多数存在します。

今回はこの中でもかなり有名な

『モンティ・ホール問題』について紹介しようと思います。

モンティ・ホール問題とは？

アメリカで放送されていた『Let's make a deal』というゲームショー番組で、

あるゲームが行われました。

このゲームは、

挑戦者が３つのドアから１つのドアを選ばさせ、そのドアの向こう側に当たりの商品もしくはハズレの商品どちらかがあるというシンプルな問題でした。

どんなゲームだったのか？

実際にどんなゲームだったのかを紹介するので、みなさんなら直感的にどれを選ぶか考えてみてください！

STEP１　

みなさんの目の前に３つのドアが現れます。

f:id:smohisano:20210830152110p:plain

このドアの向こうには、当たりの場合は「車」があり、ハズレの場合は「ヤギ」がいます。「車」を引き当てた時にのみ手に入れることができます。

f:id:smohisano:20210830152349p:plain

STEP２

この３つのドアから１つのドアを選択します。

（このとき、ドアの奥からエンジン音とかヤギの鳴き声は聞こえませんw）

f:id:smohisano:20210830152550p:plain

STEP３

次に、このゲームの司会者であるホール氏が図のようにハズレのドアを一つ教えてくれます。

（ちなみに、『モンティ・ホール問題』は司会者の名前から付けられたみたいですね。）

f:id:smohisano:20210830152852p:plain

STEP４

ここで司会者は、あなたにこう問います。

「最初に選んだ赤い矢印のドアのままにしますか？」

それとも「もう一つの緑の矢印のドアに変えますか？」

f:id:smohisano:20210830153158p:plain

STEP５

ここで、あなたに質問です。

A：「最初に選んだドアから変えません！」

B：「もう一つの空いてるドアにしようかな…」

C：「どっちにしても一緒だからどっちでもいいって！」

あなたならどれを選びますか？

天才現れる

この問題に対して、

IQ230のマリリン・ボス・サヴァントは自身が掲載するコラムにてこう言った。

「正解は、B『ドアを変える』よ。ドアを変えると変えないときにあたりを引く確率の２倍になるもの。」

んんん？？

変えた方が良い？しかも、確率が２倍になるだと？？？！！！！

この発言に対して、世界中から批判の手紙が届きました。

中には、大学の数学者からも批判が届いたらしいです。

「君は明らかなヘマをした世界最高の知能指数保有者である貴女が自ら数学的無知をこれ以上世間に広める愚行を直ちに止め、恥を知るように！」

「プロの数学者として、一般大衆の数学的知識の低さを憂慮する。自らの間違いを認める事で現状が改善されます」

散々な言われようですね…

しかし、これがきっかけで本当のところどうなのか？ということが調べられました。

解説

確率の基礎・基本を確認したい方はこちらをチェック

では、本当に変えた方が変えなかった場合の２倍の確率になるかを確認してみましょう。

解説①　理論的に理解する

$(i)$ 　最初に選んだドアから変えなかった場合に当たる確率

$(ii)$ 　もう一つのドアに変更する場合に当たる確率

この２つに場合分けして比べてみます。

ドアの配置は左からヤギ、車、ヤギだとします。

f:id:smohisano:20210901202052p:plain

$(i)$ 　最初に選んだドアから変えなかった場合に当たる確率

①のドアを選ぶ時

f:id:smohisano:20210901202245p:plain

司会者は③をハズレと教えてくれます。

その後、挑戦者は最初に選んだドアから変えないのでハズレのままです。

②のドアを選ぶ時

f:id:smohisano:20210901202815p:plain

司会者は①もしくは③をハズレと教えてくれます。

その後、挑戦者は最初に選んだドアから変えないので当たりのままです。

③のドアを選ぶ時

f:id:smohisano:20210901202955p:plain

司会者は①をハズレと教えてくれます。

その後、挑戦者は最初に選んだドアから変えないのでハズレのままです。

よって、変えなかった場合のあたる確率は、 $\dfrac{1}{3}$ となります。

> $(ii)$ 　もう一つのドアに変更する場合に当たる確率</span

①のドアを選ぶ時

f:id:smohisano:20210901202245p:plain

司会者は③をハズレと教えてくれます。

その後、挑戦者は最初に選んだドアから変えるので、当たりになります。

②のドアを選ぶ時

f:id:smohisano:20210901202815p:plain

司会者は①もしくは③をハズレと教えてくれます。

その後、挑戦者は最初に選んだドアから変えるので、ハズレになります。

③のドアを選ぶ時

f:id:smohisano:20210901202955p:plain

司会者は①をハズレと教えてくれます。

その後、挑戦者は最初に選んだドアから変えるので、当たりになります。

よって、もう一つのドアに変える場合の確率は、 $\dfrac{2}{3}$ となります。

$(i)$ 　最初に選んだドアから変えない： $\dfrac{1}{3}$

$(ii)$ 　もう一つのドアに変える： $\dfrac{2}{3}$

このように、確かにもう一つのドアに変えた場合の方が当たる確率が２倍になるみたいですね！

解説② 　ドアを100個に増やして感覚的に理解する

ここまでの内容でピンと来ない人は、ドアの数を増やしてみると良いかもしれません。

ドアが100個の場合、

最初に選んだドアから変えない方が良いのか？もう一つのドアに変えた方が良いのか？考えてみましょう。

f:id:smohisano:20210901204711p:plain

当たりのドアを①とします。

f:id:smohisano:20210901204742p:plain

最初に②のドアを選んだとします。

f:id:smohisano:20210901204808p:plain

このとき、当たりのドアと選んだドア以外のドアをハズレと教えてくれますので、

f:id:smohisano:20210901204846p:plain

このように、③から100までのドアがハズレだとわかります。

この時に、「あなたは変えますか？変えませんか？」これなら変えた方が良いというのがわかる方もいるのではないでしょうか？

以上が理論的に考えて理解する方法とドアを増やして感覚的に理解する方法でした。

おわりに

今回は、パラドックス問題の一つである「モンティホール問題」を解説してみました。

数学を勉強していくとこういった面白い問題にたくさん出会うことができて、ワクワクを得られます！

いろんな確率の問題を解説してますので、こちらも合わせてチェックしてみてください！

オンラインの家庭教師もやっていますので、気になる方はお問い合わせフォームからご連絡ください♪

お問い合わせフォーム

Math Kit

数学を学ぶためのキットが揃っています。

「途中式を飛ばさない」数学学習サイトとなっています。

ぜひ、学習に役立たせてください。

2021-08-27

ベクトルが含まれた方程式がベクトル方程式ただそれだけ

数学B 数学B-平面ベクトル

はじめに

今回は、ベクトルが含まれた方程式についての問題です。

ベクトル方程式は、ベクトルの中でも特に難しい単元ですね。

しかし、ベクトルは大きさと向きを表すものという定義をしっかりと押さえておけば決して理解できない単元ではないです！

ベクトルの定義などの基本を復習したい方はこちらをチェック

ベクトル方程式とは？

ベクトル方程式とはなにか？

難しく考えるとなんなのかがわからなくなってきます。

シンプルに考えましょう！

ベクトル方程式とは、ベクトルを含んだ方程式です。

つまり、

ベクトルでも直線の方程式とか円の方程式とかを表すことができるんだよ！ってだけの話です。

直線の方程式を求める問題は、中学生の時や数学 Ⅱ でも扱いましたね。

直線と方程式についてはこちらをチェック

直線のベクトル方程式

直線上の任意の点 $P$ の位置ベクトルを $\overrightarrow{p}$ とし、 $s$ と $t$ を実数の変数とする。

定点 $A(\overrightarrow{a})$ を通り、 $\overrightarrow{0}$ でないベクトル $\overrightarrow{d}$ に平行な直線

　 $\overrightarrow{p}=\overrightarrow{a}+t\overrightarrow{d}$ 　 $\overrightarrow{d}$ は直線の方向ベクトル

異なる $2$ 点 $A(\overrightarrow{a})$ ,　 $B(\overrightarrow{b})$ を通る直線

　 $\overrightarrow{p}=(1-t)\overrightarrow{a}+t\overrightarrow{a}$ 　または　 $\overrightarrow{p}=s\overrightarrow{a}+t\overrightarrow{a}$ 　 $s+t=1$

定点 $A(\overrightarrow{a})$ を通り、 $\overrightarrow{0}$ でないベクトル $\overrightarrow{n}$ に垂直な直線

　 $\overrightarrow{n}(\overrightarrow{p}-\overrightarrow{a})=0$ 　 $\overrightarrow{n}$ は直線の法線ベクトル

公式の説明

今回使用する公式を解説する。

定点 $A(\overrightarrow{a})$ を通り、 $\overrightarrow{0}$ でないベクトル $\overrightarrow{d}$ に平行な直線

　 $\overrightarrow{p}=\overrightarrow{a}+t\overrightarrow{d}$ 　 $\overrightarrow{d}$ は直線の方向ベクトル

f:id:smohisano:20210827144627p:plain

求めたい直線は点 $P$ の集まりです。赤線（ $\overrightarrow{p}$ ）で表しています。

点 $P$ の位置ベクトルを $\overrightarrow{p}$ と表す。そして、 $\overrightarrow{p}$ は求めたい直線上を移動します。

【目標】

「 $\overrightarrow{p}$ が直線上のどこを指していても、成り立つようなベクトルを含んだ方程式を立てる。」

f:id:smohisano:20210827144709p:plain

直線上の任意の点 $A$ の位置ベクトルを $\overrightarrow{a}$ とおくと上図のようになる。

f:id:smohisano:20210827144737p:plain

また、求めたい直線に平行なベクトル $\overrightarrow{d}$ を適当に書いておく。

すると、線分 $AP$ に $t\overrightarrow{d}$ と表すことができる。

f:id:smohisano:20210827144803p:plain

したがって、無駄な部分を排除して見てみると、

$\overrightarrow{a}$ $+$ $t\overrightarrow{d}$ $=$ $\overrightarrow{p}$

　　　 $\overrightarrow{p}$ $=$ $\overrightarrow{a}$ $+$ $t\overrightarrow{d}$

となる。

問題

点 $A(-4,$ 　 $2)$ を通り、ベクトル $\overrightarrow{d}=(3,$ 　 $-1)$ に平行な直線の方程式を求めよ。

解説

図にすると、

f:id:smohisano:20210827151114p:plain

よって、

$\overrightarrow{p}=(x,$ 　 $y)$ とすると、

$(x,$ 　 $y)=(-4,$ 　 $2)+t(3,$ 　 $-1)$

$x$ 座標と $y$ 座標それぞれを式にすると、

媒介変数を $t$ とすると、（ $\ast$ 媒介変数とは、一つの式を二つに分けるための変数）

$\begin{cases}x=-4+3t\\y=2-t\end{cases}$

$t$ を消去すると、直線の方程式が求められる

上記の解説を踏まえた上で、実際の答案を見てみましょう！

実際の答案

$\overrightarrow{p}=(x,$ 　 $y)$ とすると、

$(x,$ 　 $y)=(-4,$ 　 $2)+t(3,$ 　 $-1)$

媒介変数を $t$ とすると、

$\begin{cases}x=-4+3t\cdots①\\y=2-t\cdots②\end{cases}$

②より

$3y=6-3t$

$3t=6-3y$

①に代入すると、

$x=-4+6-3y$

$x+3y-2=0$

おわりに

今回は、ベクトルが含まれた方程式についての問題でした。

記事の問題に対して質問がある方はいつでもご連絡ください。

また、オンラインで家庭教師も可能です。

詳しくは下記の問い合わせフォームからご連絡ください。

いつでもお待ちしております。

お問い合わせフォーム

Math Kit

数学を学ぶためのキットが揃っています。

「途中式を飛ばさない」数学学習サイトとなっています。

ぜひ、学習に役立たせてください。

2021-08-24

式を図に落とし込む！位置ベクトルについての問題

数学B 数学B-平面ベクトル

はじめに

今回は、位置ベクトルについての問題です。

早速ですが、ポイントは２点あります。

①　位置ベクトルがなにかを理解する

②　式を図に落とし込む

図に落とし込むことができれば、問題を解くために必要な情報が見えてきます。

式を図に落とし込むポイント

式を図に落とし込むために、始点を変更しなければいけない場合があります。

始点の変更についてはこちらをチェック

位置ベクトルとは？

位置ベクトルとは、

$\overrightarrow{p}$ に対して、任意の点を始点（ここでは、点 $P$ とする。）にして、 $\overrightarrow{p}=\overrightarrow{OP}$ と表すことです。

よく使用する形

$\triangle{ABC}$ において、線分 $BC$ を $m$ $:$ $n$ に内分する点を $P$ とするとき、

$\overrightarrow{AP}=$ $\dfrac{n}{m+n}$ $\overrightarrow{AB}$ + $\dfrac{m}{m+n}$ $\overrightarrow{AC}$

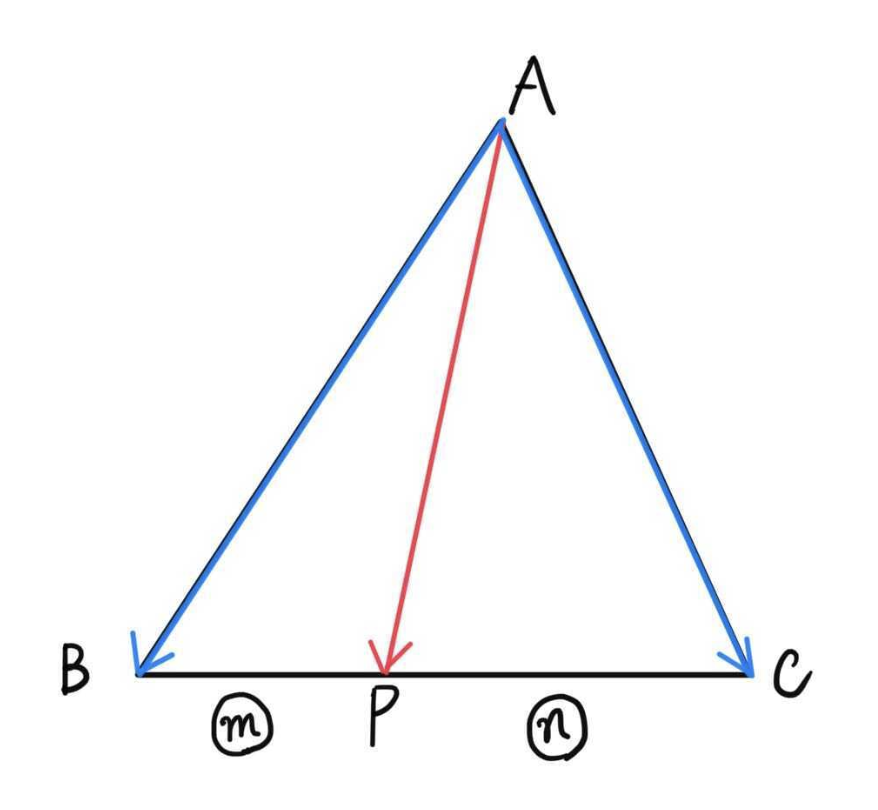
f:id:smohisano:20210824195058p:plain

はじめに
- 式を図に落とし込むポイント
- 位置ベクトルとは？
問題
解説
実際の答案
おわりに
Math Kit

問題

$\triangle{ABC}$ の内部に点 $P$ があり、 $6\overrightarrow{PA}+3\overrightarrow{PB}+2\overrightarrow{PC}=\overrightarrow{0}$ を満たすとき、

点 $P$ はどのような位置にあるか。

解説

今回の場合は、

式： $6\overrightarrow{PA}+3\overrightarrow{PB}+2\overrightarrow{PC}=\overrightarrow{0}$

図： $\triangle{ABC}$

上記の式を図に落とし込む必要があります。

そのためにまずは始点を変更してみましょう。

今回の問題の式を見てみると、始点が $P$ になっていますね。

このままだと点 $P$ の位置がよくわかりません。

点 $P$ の位置をわかりやすくするためには、

三角形の頂点を始点にしましょう。

$6\overrightarrow{PA}+3\overrightarrow{PB}+2\overrightarrow{PC}=\overrightarrow{0}$

$6(-\overrightarrow{AP})+3(\overrightarrow{AB}-\overrightarrow{AP})+2(\overrightarrow{AC}-\overrightarrow{AP})=\overrightarrow{0}$

　 $-6\overrightarrow{AP}+3\overrightarrow{AB}-3\overrightarrow{AP}+2\overrightarrow{AC}-2\overrightarrow{AP}=\overrightarrow{0}$

　　　　　　　 $11\overrightarrow{AP}=3\overrightarrow{AB}+2\overrightarrow{AC}$

　　　　　　　 $\overrightarrow{AP}=\dfrac{3}{11}\overrightarrow{AB}+\dfrac{2}{11}\overrightarrow{AC}$

　　　　　　　 $\overrightarrow{AP}=\dfrac{5}{11} \left(\dfrac{3}{5}\overrightarrow{AB}+\dfrac{2}{5}\overrightarrow{AC}\right)$

ここまで整理できたら、図に落とし込みましょう。

$\overrightarrow{AD}=\dfrac{3}{5}\overrightarrow{AB}+\dfrac{2}{5}\overrightarrow{AC}$ とおくと、

点 $D$ は、 $\triangle{ABC}$ において線分 $BC$ を $2$ $:$ $3$ に内分する点とわかる。 $\cdots$ ①

① より

f:id:smohisano:20210822162028p:plain

また、

$\overrightarrow{AP}=\dfrac{5}{11} \overrightarrow{AD}$

と表されるので、

点 $P$ は、 $\triangle{ABC}$ において線分 $AD$ を $5$ $:$ $6$ に内分する点とわかる。 $\cdots$ ②

② より

f:id:smohisano:20210822162050p:plain

点 $P$ は、 $\triangle{ABC}$ において線分 $AD$ を $5$ $:$ $6$ に内分する点とわかる。 $\cdots$ ②

ここまでの内容を踏まえた上で実際の答案を見ていきましょう。

実際の答案

$6\overrightarrow{PA}+3\overrightarrow{PB}+2\overrightarrow{PC}=\overrightarrow{0}$

$6(-\overrightarrow{AP})+3(\overrightarrow{AB}-\overrightarrow{AP})+2(\overrightarrow{AC}-\overrightarrow{AP})=\overrightarrow{0}$

　 $-6\overrightarrow{AP}+3\overrightarrow{AB}-3\overrightarrow{AP}+2\overrightarrow{AC}-2\overrightarrow{AP}=\overrightarrow{0}$

　　　　　　　 $11\overrightarrow{AP}=3\overrightarrow{AB}+2\overrightarrow{AC}$

　　　　　　　 $\overrightarrow{AP}=\dfrac{3}{11}\overrightarrow{AB}+\dfrac{2}{11}\overrightarrow{AC}$

　　　　　　　 $\overrightarrow{AP}=\dfrac{5}{11} \left(\dfrac{3}{5}\overrightarrow{AB}+\dfrac{2}{5}\overrightarrow{AC}\right)$

$\overrightarrow{AD}=\dfrac{3}{5}\overrightarrow{AB}+\dfrac{2}{5}\overrightarrow{AC}$ とおくと、

$\overrightarrow{AP}=\dfrac{5}{11} \overrightarrow{AD}$

と表される。よって、

$\triangle{ABC}$ において線分 $BC$ を $2$ $:$ $3$ に内分する点を点 $D$ とすると、

点 $P$ は、線分 $AD$ を $5$ $:$ $6$ に内分する点である。

おわりに

今回は、位置ベクトルについての問題でした。

記事の問題に対して質問がある方はいつでもご連絡ください。

また、オンラインで家庭教師も可能です。

詳しくは下記の問い合わせフォームからご連絡ください。

いつでもお待ちしております。

お問い合わせフォーム

Math Kit

数学を学ぶためのキットが揃っています。

「途中式を飛ばさない」数学学習サイトとなっています。

ぜひ、学習に役立たせてください。

2021-08-20

絶対値がついたら２乗！ベクトルの大きさの最小値問題

数学B 数学B-平面ベクトル

問題

ベクトル $\overrightarrow{a}$ ,　 $\overrightarrow{b}$ について $|\overrightarrow{a}|=\sqrt{3}$ ,　 $|\overrightarrow{b}|=\sqrt{2}$ ,　 $|\overrightarrow{a}-\overrightarrow{b}|=\sqrt{5}$ であるとき

(1)　内積 $\overrightarrow{a}\cdot \overrightarrow{b}$ の値を求めよ。

(2)　ベクトル $|2\overrightarrow{a}-3\overrightarrow{b}|$ の大きさを求めよ。

(3)　ベクトル $|\overrightarrow{a}+t\overrightarrow{b}|$ の大きさが最小となるように実数 $t$ の値を定め、そのときの最小値を求めよ。

つまずきポイント

今回は、ベクトルの大きさの最小値問題です。

ベクトルの大きさが与えられているときの解法を覚えていないと、

手も足も出ない問題かもしれません。

今回の問題のポイント

ベクトルの大きさが与えられていたら２乗しましょう。

問いの中にあるこちらの式は、このままだとなにも計算ができません。

$|\overrightarrow{a}-\overrightarrow{b}|=\sqrt{5}$

両辺を２乗することによって、

$\overrightarrow{a} \cdot\overrightarrow{b}$ の値を求めることができ、(2) にも繋がります。

二次関数の最小値問題

(3)では、(2)と同様に計算をし、

式を整理することができたら二次関数の最小値を求めなければいけません。

二次関数の最小値問題が不安な方はこちらをチェックしてみてください。

解説

(1)

$|\overrightarrow{a}-\overrightarrow{b}|^2=(\sqrt{5})^2$

$|\overrightarrow{a}|^2-2\overrightarrow{a} \cdot\overrightarrow{b}+|\overrightarrow{b}|^2=5$

$|\overrightarrow{a}|=\sqrt{3}$ ,　 $|\overrightarrow{b}|=\sqrt{2}$ より

$(\sqrt{3})^2-2\overrightarrow{a} \cdot\overrightarrow{b}+(\sqrt{2})^2=5$

$3-2\overrightarrow{a} \cdot\overrightarrow{b}+2=5$

　　 $-2\overrightarrow{a} \cdot\overrightarrow{b}=0$

　　　 $\overrightarrow{a} \cdot\overrightarrow{b}=0$ $\cdots$ $\ast$

(2)

　 $|2\overrightarrow{a}-3\overrightarrow{b}|^2$

$=2^2|\overrightarrow{a}|^2-12\overrightarrow{a} \cdot \overrightarrow{b}+3^2|\overrightarrow{b}|^2$

　 $|\overrightarrow{a}|=\sqrt{3}$ ,　 $|\overrightarrow{b}|=\sqrt{2}$ と (1) の $\ast$ より

$=4 (\sqrt{3})^2-12 \cdot 0+9(\sqrt{2})^2$

$=4\cdot 3+9\cdot 2$

$=30$

よって、

$|2\overrightarrow{a}-3\overrightarrow{b}|=\sqrt{30}$

（最初に $2$ 乗していることを忘れずに）

(3)

　 $|\overrightarrow{a}+t\overrightarrow{b}|^2$

$=|\overrightarrow{a}|^2+2t\overrightarrow{a} \cdot\overrightarrow{b} +t^2 |\overrightarrow{b}|^2$

$|\overrightarrow{a}|=\sqrt{3}$ ,　 $|\overrightarrow{b}|=\sqrt{2}$ と (1) の $\ast$ より

$=3+2t^2$

$=2t^2+3$

頂点 $(0,$ 　 $3)$

よって、

$t=0$ のとき最小値 $\sqrt{3}$

おわりに

今回は、ベクトルの大きさの最小値問題でした。

ベクトルの基本知識はもちろんのこと、二次関数の最小値問題の解法も覚えている必要があります。

もっと詳しく教えてほしいという方は、

下記の問い合わせフォームからご連絡ください。

いつでもお待ちしております。

お問い合わせフォーム

Math Kit